How to use Theta to Trade Options?

Theta options represent a Greek parameter used to gauge the speed at which an option sheds its time-related worth as it approaches its expiration date. Essentially, it quantifies the rate of reduction in an option's price over time, a phenomenon commonly known as time decay in the context of option contracts.

The fundamental premise underlying Theta options is the anticipation that, assuming all other factors remain constant, an options contract will inevitably lose value and become less appealing to investors as it nears its maturity. Theta in options is consistently expressed as a negative figure, as it is subtracted from the monetary value of the options contract on any given day. For instance, if Theta is -3 and all other variables remain unchanged, the option's value for that specific day will diminish by 3 points.

How to Interpret Theta:

Theta in options consistently signifies the diminishing value and the exposure to time-related risk within an options contract, manifesting as a perpetually negative value. 

In the context of long options, the persistence of a negative Theta implies that, upon expiration, the option's time value reaches zero. Consequently, this dynamic results in an advantageous scenario for option sellers, leading to an increase in value for them. 

Conversely, it corresponds to a simultaneous decrease in value for option buyers. This characteristic establishes theta as a favorable technical factor for option sellers, labeling the act of selling an option as a positive theta trade, while buying an option is deemed a negative theta trade.

How to Calculate Theta in Options:

The calculation of Theta involves both negative and positive values depending on the position's time frame in options trading. Specifically, Theta is negative for long positions and positive for short positions. To determine the Theta value, utilize the formula provided below:

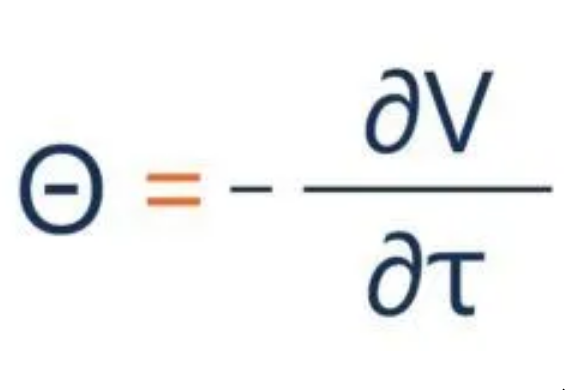
Where:

∂ – the first derivative

V – the option’s price (theoretical value)

τ – the option’s time to maturity

In the Black-Scholes model, the formula for calculating theta is as follows:

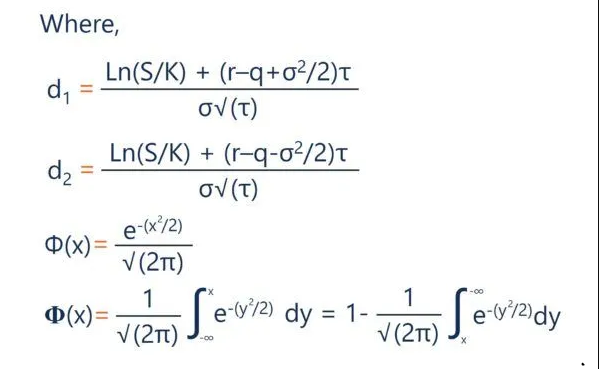
Where:

S – the stock price

K – the strike price

r – the risk-free rate

q – the annual dividend yield

τ – time until expiration

σ, the volatility

Utilizing Theta in Trading Strategies

Theta holds particular significance for traders employing strategies in a neutral market, as these approaches aim to profit from the impact of time decay.

In such strategies, it is imperative to ensure that the overall theta value of your position is appropriately managed to capitalize on diminishing extrinsic value. If time decay negatively affects your position, reliance on directional moves in the underlying security becomes necessary for profitability, thereby compromising the essence of these strategies.

Traders focusing on profiting from substantial directional moves in underlying securities, or those intending to hold positions until expiration, have less concern about theta. The loss of extrinsic value in such trades is viewed as a direct cost of the trade, expected to be balanced by profits generated from relevant directional moves.

In these instances, Delta becomes more relevant, although it is advisable to check theta values to understand potential time decay effects.

Theta becomes highly relevant for traders entering positions anticipating small directional movements in underlying securities over a relatively short period. To profit from such positions, the gain in intrinsic value must exceed the loss of extrinsic value.

For optimal results when speculating on small movements, it is preferable to trade options with low theta values. This precaution prevents time decay from eroding profits arising from these minor market fluctuations. Thus, a comprehensive understanding of theta and its implications is essential for informed decision-making in trading activities.

Key Takeaways:

• Theta measures how fast an option loses value due to time decay.

• Negative Theta is typical, indicating a daily subtraction from the option's value.

• It is crucial for traders in neutral strategies to capitalize on time decay effects.

• Traders need to manage overall theta to benefit from diminishing extrinsic value.

• For small directional movements, trading options with low theta values help prevent time decay from eroding profits.

Frequently Asked Questions:

1. What is theta in options and can you provide an example?

Theta in options is always a negative number, subtracted from the rupee value of the options contract daily.

For instance, if theta is -3 with constant variables, the option value erodes by 3 points on that particular day.

2. Is a high theta good for options?

• Yes, a higher theta indicates that the option's value will decay more rapidly as the expiration date approaches.

• Theta behaves nonlinearly, accelerating the decay of options over time.

3. How does option theta work?

Theta represents the theoretical daily decrease in an option's price, assuming all other factors remain constant.

For example, a theta of -0.05 implies a 5-cent decrease per day in the option's price due to time decay.

4. How is theta value calculated?

Theta: Θ=∂P∂t

Theta is typically negative, signifying a decline in the option premium over time.

Calculated in years, dividing theta by 252 provides the daily decline in the option premium due to time decay.

5. What are the Greek options in Banknifty?

• Delta, Gamma, Vega, Theta, and Rho are the five prominent risk indicators collectively known as Greeks.

• As option Greeks, each is crucial for indicating the sensitivity of the option value to changes in the underlying asset's price.