How To Calculate Gamma for Options Trading

What Is Gamma in Options Trading

In option trading, gamma is a measurement of how much the delta of an option changes in response to a one-point movement in the underlying asset. Delta measures the sensitivity of an option's price to changes in the price of the underlying security. Gamma, on the other hand, quantifies the rate of change of delta. It is also known as delta of the delta.

Key Points About Gamma Strategy in Options Trading

Dynamic Nature: Gamma is dynamic and changes as the price of the underlying asset, time to expiration, and implied volatility change. It is highest for at-the-money options and decreases as options move further in or out of the money.

Effect on Delta: Gamm is directly related to delta. If you think of delta as the speed at which an option's price changes with respect to changes in the underlying asset's price, gamma is the acceleration of that speed. In other words, gamma measures how quickly delta changes.

Hedging: Gamma is crucial for options traders who engage in dynamic hedging. When traders use options to hedge their positions, they may adjust their positions as the underlying asset's price changes. Understanding gamma helps traders anticipate and manage changes in delta, enabling more effective hedging strategies.

Impact on Profits and Losses: Gamma can have a significant impact on profits and losses. A positive gamma (common for long options positions) means that as the underlying asset's price increases, delta increases, leading to potential profits. Conversely, a negative gamma (common for short options positions) means that as the underlying asset's price increases, delta decreases, potentially leading to losses.

Time Sensitivity: Gamma is also related to the concept of theta, which measures the sensitivity of an option's price to the passage of time. Gamma tends to be higher for options with more time to expiration, making it a factor to consider when evaluating longer-term options positions.

Options Pricing Models: Gamma is a key component in options pricing models, such as the Black-Scholes model. Understanding gamma is essential for pricing options accurately and managing risk effectively.

What Does Gamma Mean in Options Trading

Interpreting gamma options in trading involves understanding how it influences the behaviour of an option's delta and, consequently, its sensitivity to changes in the price of the underlying asset. Here are key points to consider when interpreting gamma:

Delta Sensitivity: Unveiling the Rate of Change

Gamma measures the rate of change of delta. Delta, in turn, represents how much an option's price is expected to change for a one-point change in the price of the underlying asset.

A positive gamma implies that as the underlying asset's price increases, the delta of a call option increases. Conversely, as the underlying asset's price decreases, the delta decreases.

A negative gamma implies that as the underlying asset's price increases, the delta of a put option decreases. Conversely, as the underlying asset's price decreases, the delta increases.

Accelerated Price Sensitivity: Understanding Gamma's Impact on Delta

Gamma represents the acceleration of delta. In practical terms, this means that as the underlying asset's price changes, the delta of an option will change more rapidly if gamma is higher.

At-the-Money vs. Out-of-the-Money: Gamma's Gradient in Options

Gamma is typically highest for at-the-money options and decreases as options move further in or out of the money. This is important for traders to consider when selecting options based on their risk tolerance and market outlook.

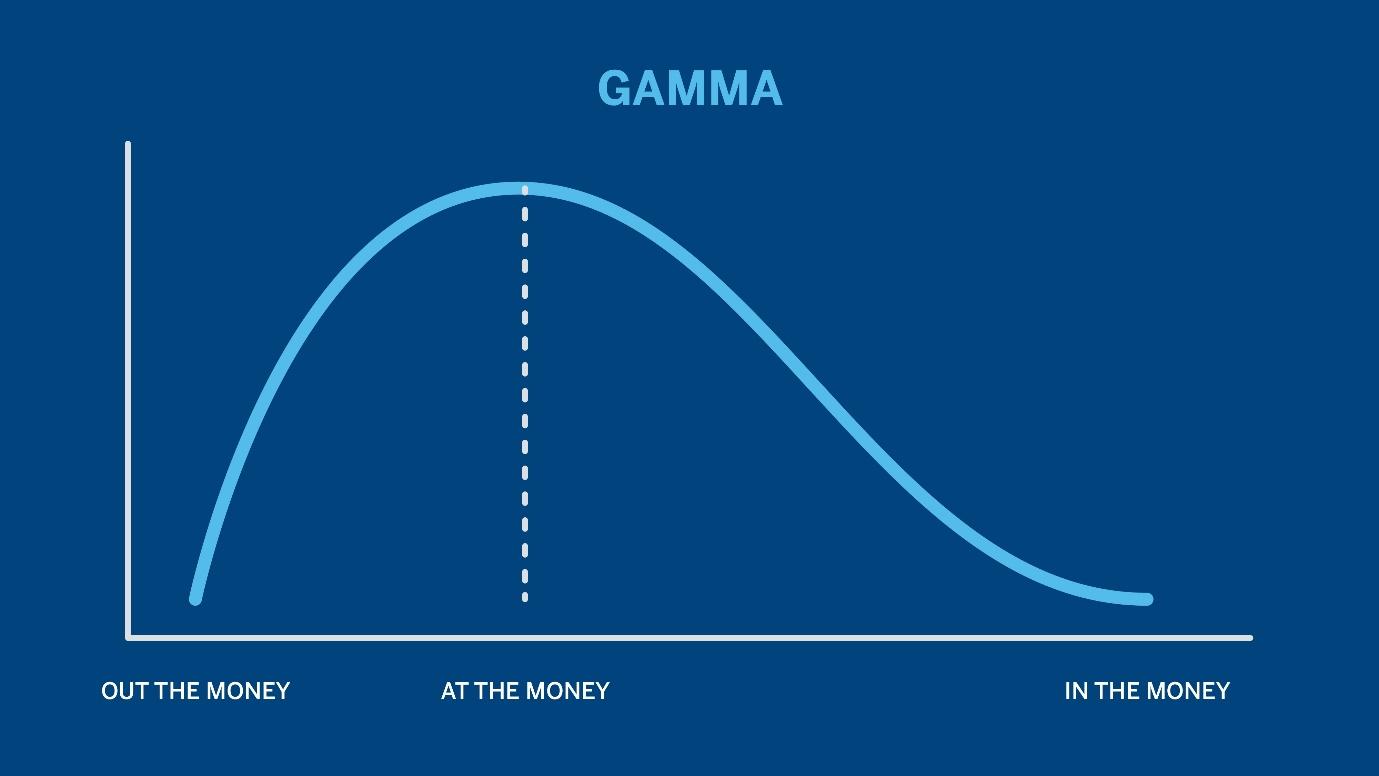
Image shows that the Gamma is highest for at the money options

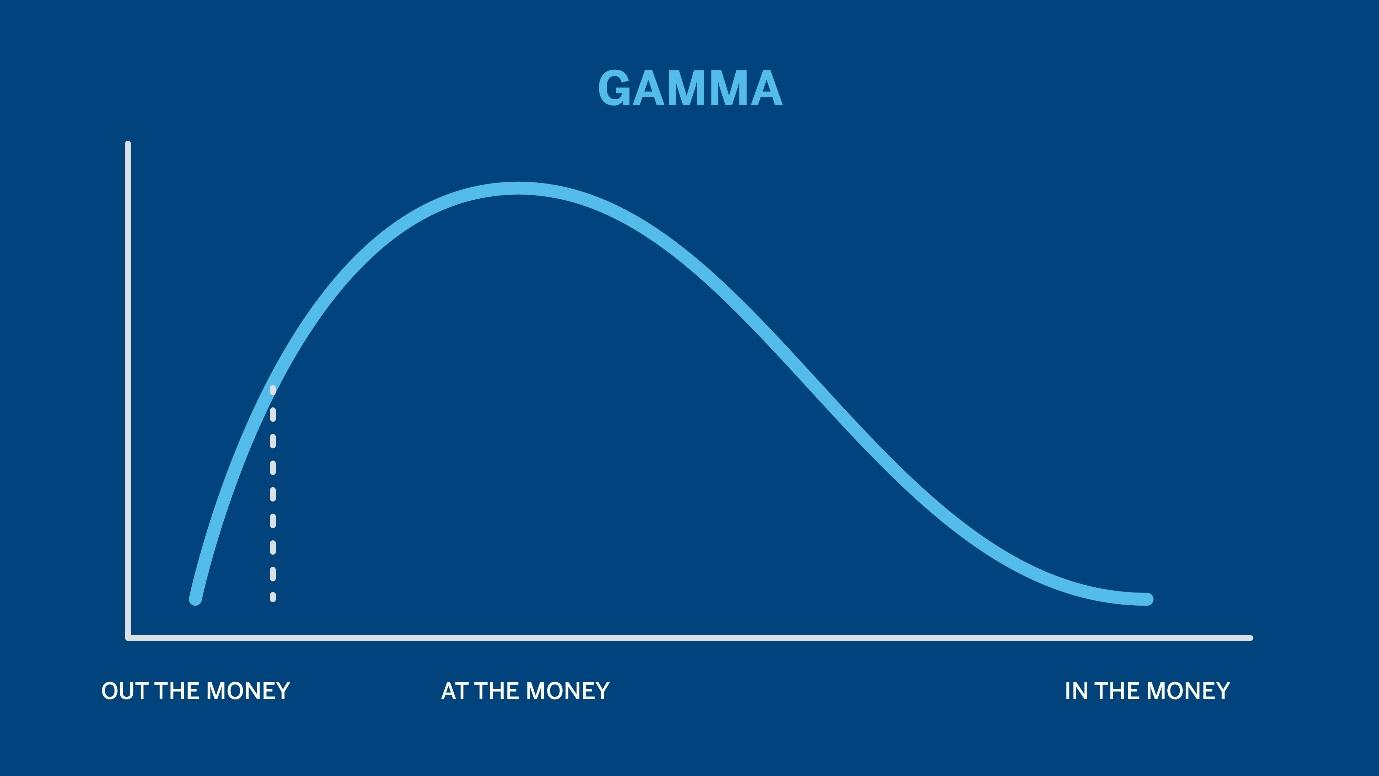
Image shows that the Gamma decreases as options move further to out the money or in the money 

Dynamic Hedging: Leveraging Gamma for Timely Adjustments

For traders engaged in dynamic hedging strategies, gamma is a critical parameter. If you're using options to hedge a portfolio, understanding how gamma affects delta helps in making timely adjustments to maintain the desired level of hedging.

Risk Management: Navigating High Gamma Positions

Gamma has implications for risk management. A high gamma position can result in larger losses (or gains) if the underlying asset's price experiences rapid and significant changes.

Traders need to be aware of their overall gamma exposure, especially in complex options strategies, to manage risks effectively.

Time Sensitivity: Gamma's Role in Longer-Term Options

Gamma tends to be higher for options with more time to expiration. This is important for traders considering longer-term options positions because the rate of change in delta is more significant with the passage of time.

Options Pricing Models: Gamma's Significance in Valuation

Understanding gamma is integral to options pricing models such as the Black-Scholes model. It contributes to determining the fair value of an option and aids in assessing the impact of changes in market conditions on option prices.

Understand 

How To Calculate Gamma 

Determining gamma involves intricate processes, necessitating the use of financial software or spreadsheets to obtain an accurate value. However, the subsequent example illustrates an approximate computation of gamma.

Consider an underlying asset whose

Delta - 40

Current asset value = 200

If value moves to 201, Then delta changes to – 43

If the value moves down to 199, Then delta changes to – 37

Then Approximate value of Gamma is 

 

How To Calculate Gamma for Options Trading

Kindly recall that Gamma is a measure of how much an option's delta changes in response to a one-point movement in the underlying asset. It's an important risk parameter for options traders, especially those engaged in dynamic hedging strategies. The gamma of an option is highest for at-the-money options and decreases as options move further in or out of the money.

Here's how you can calculate gamma for options trading:

Option Gamma Formula:

How to Calculate Gamma for Options Trading

Calculate Delta:

For a call option, delta is positive and ranges from 0 to 1.

For a put option, delta is negative and ranges from 0 to -1.

Delta can be calculated using option pricing models like the Black-Scholes model. 

Delta=N(d1?)

where N(d1?) is the cumulative distribution function of the standard normal distribution and d1? is part of the Black-Scholes formula.

Determine the Stock Price (S):

Use the current market price of the underlying asset.

Determine Implied Volatility (IV):

Implied volatility is an estimate of how much the underlying asset will move in the future. It's not directly observable and is often determined using option pricing models.

Determine Time to Expiration (T):

Time to expiration is usually expressed in years. 

For example, if an option has 30 days until expiration, T would be 30/365?.

Plug Values into the Gamma Formula:

Gamma =     Δ2 

--------------

S – IV * √T-

Substitute the values of Δ, S, IV, and T into the formula.

Calculate Gamma:

Use a calculator or a spreadsheet program to perform the calculation.

Example: 

Suppose you have a call option 

Delta (Δ) - 0.60

Underlying asset value (S) - $50

Implied volatility (IV) - 20%

Time to expiration (T) - 60 days until expiration.

  0.60 * 0.60

                    Gamma = ------------------------------ = 

         50 – 0.20 * √ (60/365)

After plugging in the values, you can calculate the gamma.

Remember that gamma is dynamic and can change as the underlying stock price, implied volatility, and time to expiration change. Traders often monitor gamma as part of their risk management strategy, especially if they are using options to hedge other positions.

Trading in the Indian Stock Market using Gamma

Delta itself shows the impact of the change in underlying asset price on the option; on the other hand, Gamma shows the movement of Delta itself, given the difference in the value of the underlying asset.

Gamma is a vital stock trading analytical tool and determinant in evaluating the likely impact of price changes of the underlying assets on an option for an option buyer or seller.

Gamma is a positive number regardless of the fact whether you are buying calls or puts and ranges from 0 to a maximum of 1 as Delta itself will never cross

Gamma can be negative when you are writing options. Gamma can be used to examine Delta effects and succeeding stock price changes and their impact on the options held by the investor.

Gamma works enhanced and becomes more significant in the usage of spreads and applying a more composite approach.

The relationship between Gamma and Delta becomes significant by using multiple open positions to consider the movement of the underlying security price. Gamma has a direct relationship with Delta, but there is also a co-relation between Gamma and Theta.

Usually, a high Gamma is conveyed by a high Theta. The higher the Gamma, the higher the exponential profits, provided that the underlying security or asset moves in a positive direction.

Conversely, such options have a high theta value where the time value basis decay is quicker.

Frequently Asked Questions

How do traders use Gamma for Options Hedging?

Gamma hedging aims to uphold a consistent delta in an options position, achieved through the strategic buying and selling of options to offset each other and maintain a net gamma close to zero. The resulting state, known as gamma-neutral, ensures a delicate balance in the position. Traders often seek to achieve zero gamma in conjunction with a delta-neutral (zero-delta) position, employing delta-gamma hedging. Delta-gamma hedging involves closely managing both net delta and net gamma to keep them near zero, offering protection against price fluctuations in the underlying asset. This meticulous approach immunizes the value of the options position from adverse changes in the underlying asset's price.

What is Gamma blast in options?

Gamma represents the rate of premium change for each fluctuation in the underlying asset's value. It is the factor influencing options to exhibit characteristics akin to lottery tickets. The phenomenon known as Gamma Blast in trading and it is accountable for the rapid and substantial multiplication of the value of options tied to the underlying asset, particularly observed on the day of expiration, transforming them within minutes. This phenomenon is also called as Gamma Explosion Options. 

How to use Gamma blast strategy in Options Trading?

Gamma blast in stock market can be strategized by utilizing the best available analytics to identify a stock with the potential to shift from its current price to either the next higher Call strike or the next lower Put strike. Once prepared, initiate the trade with a stop-loss. If the strategy unfolds as planned, one might witness premiums reaching 2-3 times the entry premiums. It's advisable to adhere to a stop loss in the underlying asset. Ideally, these trades are meant for intraday, and it is recommended to close the position before the market concludes. 

How to use gamma in option trading?

Delta Hedging: Utilize gamma to adjust and manage delta through frequent delta hedging, buying or selling the underlying asset to offset changes in an option's sensitivity to price movements.

Exploit Volatility: Capitalize on periods of high volatility as gamma becomes more influential, providing opportunities for profit during rapid price changes in the underlying asset.

Maintain Gamma-Neutral Positions: Strive for gamma-neutral positions to reduce exposure to sudden market movements, actively adjusting options portfolios to optimize risk and reward.

What Is Gamma 2 Strategy in Options?

The "Gamma 2" strategy in options involves holding a portfolio of long options with a gamma value approximately twice that of the short options, aiming to capitalize on accelerated delta changes in response to small underlying asset price movements. This strategy is designed to enhance the potential for profits from dynamic adjustments in market conditions.

What Are Greek Indicators?

It is essential for a person looking to make profits from online trading in the options market to understand all the 'Greek' indicators to take out the maximum of what options have to present. Good learning of these risk indicators can assist investors in making informed trading decisions.